
 | |
Дисциплины | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
Книги | |
 | |
 | |
 | |
Разное | |
 | |
 | |
 | |
 | |
Связь | |
 | |
 | |
| Динамическое программирование (Условия задач 1-5) |
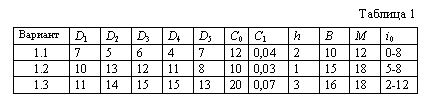
| I Варианты 1.1 - 1.3 В каждый месяц планового периода известен спрос на машины Dt(t=1,..,T), которые выпускает предприятие. Запас машин на складе предприятия составляет единиц на начало периода планирования. Общие затраты предприятия складываются из затрат на производство машин С(Х) и затрат на их содержание на складе. Пусть затраты на производство одной машины определяются выражением С(х)=С0-С1Х2, а затраты на хранение одной машины в течение месяца равны h. Месячное производство машин ограничено величиной В, а на складе можно хранить не более М машин. Отправка потребителю производится в конце месяца, а выпуск машин - равномерно в течение каждого месяца. Требуется определить оптимальный план выпуска машин, а также вычислить максимальные потери от неоптимальности. Значения параметров по вариантам даны в табл. 1. |
 |
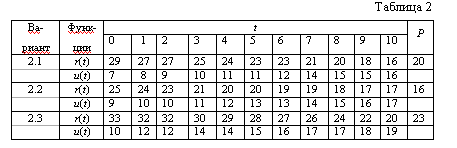
| II Варианты 2.1 - 2.3 Характеристики оборудования зависят от его возраста t: r(t) - стоимость ежегодно производимой продукции; u(t) - годовые эксплуатационные затраты; s(t) - остаточная стоимость (выручка от продажи оборудования). На начало планового периода из N лет оборудование имеет возраст t=t0. В начале любого года оборудование можно сохранить или продать и купить такое же новое по цене P (включая установку и пр.). Продолжительность замены много меньше года. Необходимо разработать оптимальную политику замены оборудования и сравнить её с наихудшей. Исходные данные приведены в табл. 2. t0=0...6; N=10. Примечание: рассматривается замена одной единицы оборудования. |
 |
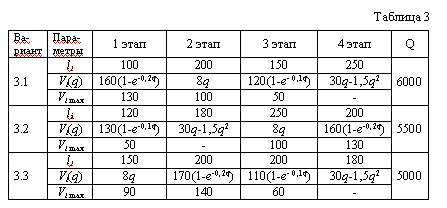
| III Варианты 3.1 - 3.3 Автомобиль должен пройти 4 этапа длиной li километров каждый. Известны зависимость скорости движения автомобиля Vi (км/ч) от расхода горючего q (л/км) для каждого этапа. Скорость движения на трех этапах ограничена. Эти данные представлены в табл. 3. Необходимо определить скорости движения, обеспечивающие минимальное время пробега при заданном количестве горючего Q (л). Показать, как отразится на решении изменение Q на 10% в обе стороны.. |
 |
| IV Варианты 4.1 - 4.3 Планируется деятельность предприятия на 5 лет. Известны функции дохода ri(xi) предприятия в i-м году (хi - количество средств, вкладываемых в i-м году). Требуется распределить имеющиеся средства в количестве Q условных единиц по годам планируемого периода, если часть дохода Р текущего года вкладывается в последующие годы, и вкладывать в год нужно не менее двух единиц средств. Как изменится решение, если снять последнее условие? Все исходные данные представлены в табл. 9. . |
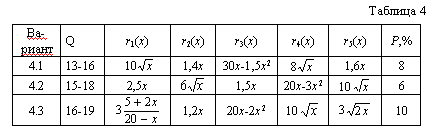 |
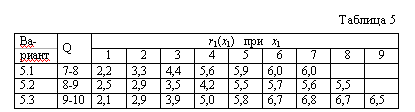
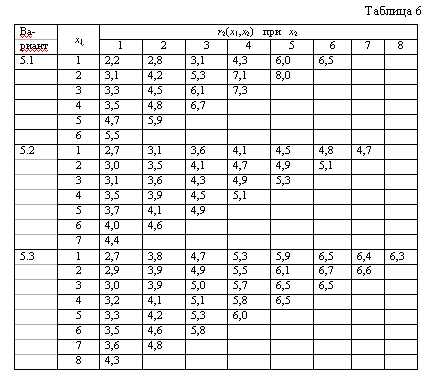
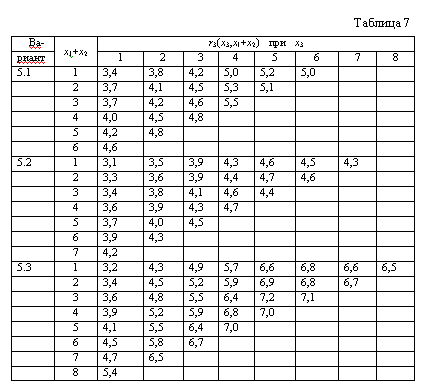
| IV Варианты 5.1 - 5.3 Планируется деятельность предприятия на 5 лет. Известны функции дохода ri(xi) предприятия в i-м году (хi - количество средств, вкладываемых в i-м году). Требуется распределить имеющиеся средства в количестве Q условных единиц по годам планируемого периода, если часть дохода Р текущего года вкладывается в последующие годы, и вкладывать в год нужно не менее двух единиц средств. Как изменится решение, если снять последнее условие? Все исходные данные представлены в табл. 9. . |
 |
 |
 |
Популярные услуги | |
 |
|
 |
|
Контакты | |
lab4students@yandex.ru | |
icq 360-992-443 | |
Обмен ссылками | |
Код для размещения(обмена) ссылки: | |