
 | |
Дисциплины | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
Книги | |
 | |
 | |
 | |
Разное | |
 | |
 | |
 | |
 | |
Связь | |
 | |
 | |
| Динамическое программирование (Условия задач 26-30) |
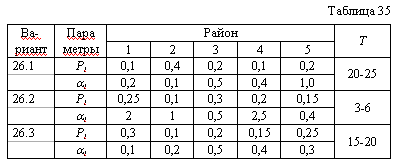
| XXI Варианты 26.1 - 26.3 Потерпевший аварию самолет может находиться в одном из n районов с вероятностями р1,...,рn. Если на поиск в i-м районе затрачивается t единиц времени, то вероятность обнаружения самолета равна 1-е-at (если самолет окажется в данном районе). Определить оптимальную стратегию поиска при условии ограничения времени поиска величиной Т. Необходимые данные приведены в табл. 35. |
 |
| XXII Варианты 27.1 - 27.3 Отрасль выпускает n типов станков. Станок типа L выполняет L-ю, L+1-ю ,..., n-ю операции. Пусть bL - потребность в станках, выполняющих L-ю операцию, L=1,2,3,...,n, а CL(x) - функция стоимости х станков типа L. Определить оптимальный вариант приобретения станков, если CL(x)=aLxb. Все данные приведены в табл. 36. |
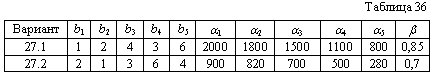 |
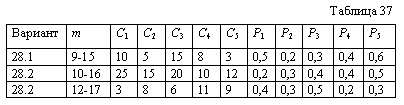
| XXIII Варианты 28.1 - 28.3 Для уничтожения n целей имеется m ракет. Значимость i-й цели оценивается величиной Ci, а вероятность поражения цели при использовании одной ракеты равна Pi (табл. 37). Определить оптимальное распределение ракет по целям. |
 |
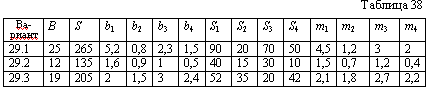
| XXIX Варианты 29.1 - 29.3 Для оснащения нового печатного цеха, имеющего производственную площадь S (м2), выделено В млн. руб. Можно приобретать станки четырех типов с одинаковыми функциями. Станок i-го типа стоит bi млн. руб., занимает площадь Si (м2) и имеет производительность mi (табл. 38). Определить оптимальный вариант оснащения цеха. . |
 |
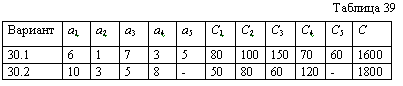
| XXV Варианты 30.1 - 30.3 Ежемесячно требуется поставлять со склада ai деталей i-го типа стоимостью Ci. Общая стоимость деталей, хранимых на складе, не должна превышать величину С (табл. 39). Определить количество хранимых деталей каждого типа, наименее уклоняющееся от потребности в них. Решить для двух показателей (раздельно), характеризующих меру уклонения. |
 |
Популярные услуги | |
 |
|
 |
|
Контакты | |
lab4students@yandex.ru | |
icq 360-992-443 | |
Обмен ссылками | |
Код для размещения(обмена) ссылки: | |