
 | |
Дисциплины | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
Книги | |
 | |
 | |
 | |
Разное | |
 | |
 | |
 | |
 | |
Связь | |
 | |
 | |
| Динамическое программирование (Условия задач 21-25) |
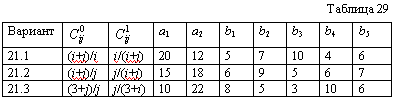
| XXI Варианты 21.1 - 21.3 Пять предприятий получают сырье с двух складов. Затраты на перевозку единицы груза от склада к предприятию зависят от количества перевозимого груза: . Пусть bj - потребность j-го предприятия в сырье, аi - количество сырья на i-м складе, при этом общий запас на складах равен суммарной потребности предприятий. Определить оптимальный план перевозок сырья для данных, приведенных в табл. 29. |
 |
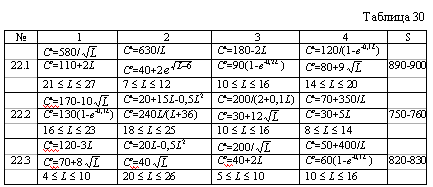
| XXII Варианты 22.1 - 22.3 Прокладывается автомобильная дорога, которая должна связать пять пунктов. Длина каждого из 4 участков дороги Li ограничена сверху и снизу. Капитальные и эксплуатационные затраты зависят от длины участка: с увеличением Li первые уменьшаются (сокращается объем земляных и мостостроительных работ), а вторые возрастают (табл. 30). Определить вариант дороги, обеспечивающий общую минимальную длину в пределах выделенных средств S. Записать функциональное уравнение для случая минимизации средств при заданной длине. Примечание: для упрощения расчетов считать, что эксплуатационные затраты даны на весь период эксплуатации дороги. |
 |
| XXIII Варианты 23.1 - 23.3 Пусть непилотируемый летательный аппарат, запускаемый с земли, должен за время Т, кратное dt, достигнуть высоты Н. Сигнал коррекции траектории поступает через интервалы dt и мгновенно отрабатывается. Между корректировками полет идет под одним углом к горизонту. Известны зависимости: q = a0+a1a2-a2h, v = b0-b1a, где q - расход горючего , кг/с; h - высота аппарата относительно земли, м; v - скорость полета, км/ч; a - угол подъема (спуска), град. Кроме того, известны стоимость горючего Сг и затраты на одну корректировку Ск (табл. 31). Требуется найти оптимальные траектории полета при 1, 2 и 3 корректировках за полет, построить графики траекторий в координатах “высота-время” и “высота-расстояние по земле от точки старта”, определить наилучшее число корректировок среди указанных значений. Точность определения траектории - не хуже 4% от Н. |
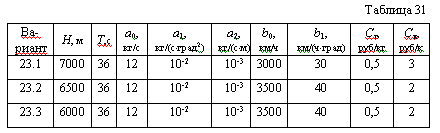 |
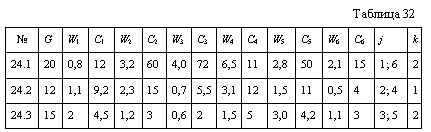
| XXIX Варианты 24.1 - 24.3 Самолет имеет максимальную грузоподъемность G(т). Предметы, загружаемые в самолет, имеют различные веса и стоимости: wi(т), Сi (руб.) соответственно (табл. 32). Определить оптимальную загрузку самолетов с грузоподъёмностью от G до 1,3G. Показать, как изменится решение, если j-х предметов нужно погрузить не меньше k. . |
 |
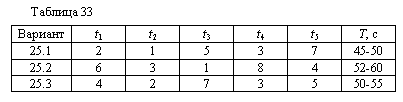
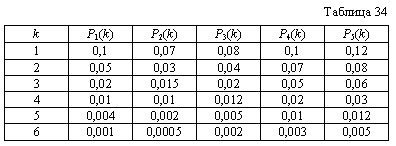
| XXV Варианты 25.1 - 25.3 На обработку информации выделено Т единиц времени. Обработка производится пятью последовательно включенными вычислительными устройствами (ВУ). Известна продолжительность однократного счета на каждом из ВУ - ti (табл. 33). Для повышения достоверности обработки применяется повторный счет на отдельных ВУ. Зависимость вероятности искажения информации от числа повторностей счета Pi(k) приведена в табл. 34. Определить оптимальный вариант обработки информации. Вывести функциональное уравнение для случая, когда задана общая допустимая вероятность искажения и необходимо минимизировать время обработки. |
 |
 |
Популярные услуги | |
 |
|
 |
|
Контакты | |
lab4students@yandex.ru | |
icq 360-992-443 | |
Обмен ссылками | |
Код для размещения(обмена) ссылки: | |